문제

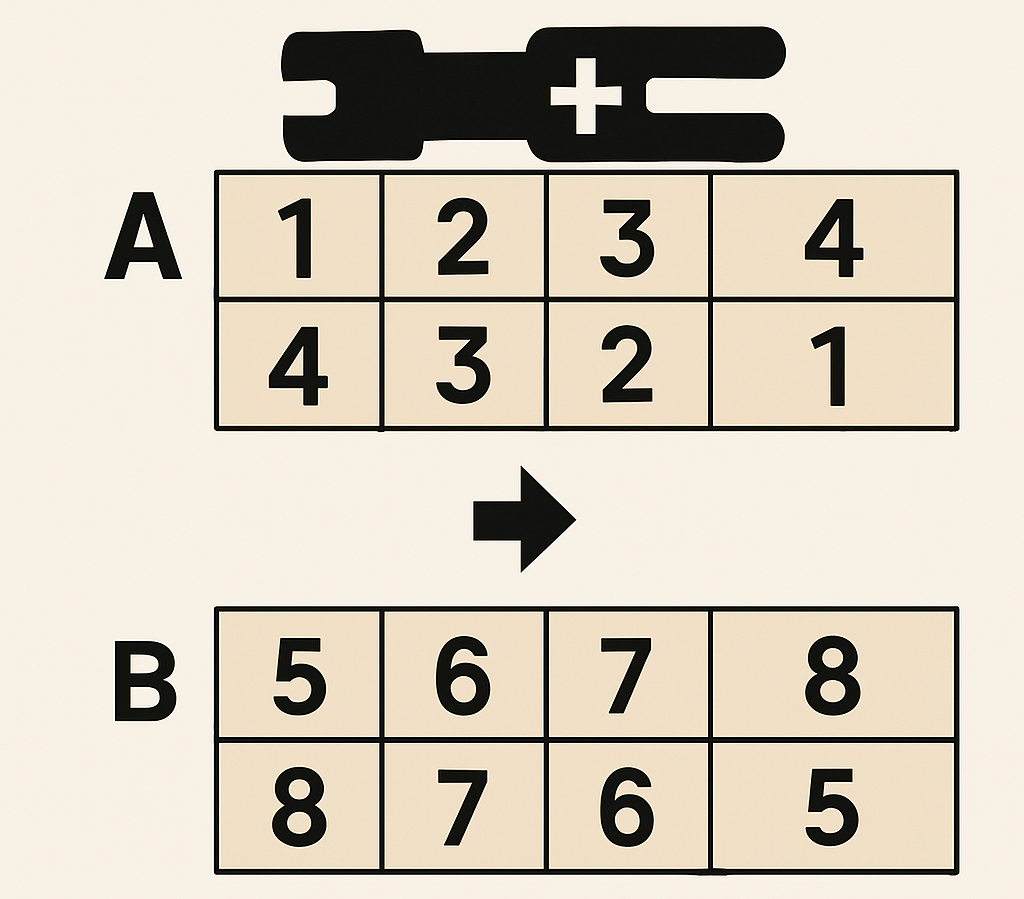
\(2\times N\) 행렬 \(A\)가 주어진다. 이 행렬의 \(r\)행 \(c\)열에 있는 원소는 \(A_{r,c}\)로 표현한다. 이 행렬을 잘 다듬어서 \(2\times N\) 행렬 \(B\)로 만들어보자. 여러분이 행렬을 다듬을 때, 사용할 수 있는 도구는 다음과 같다.

• 일반 도구: 행렬의 인접한 두 원소를 둘다 \(1\)만큼 증가시키거나 감소시키는 도구이다. 즉, \(A_{1,i}(1\le i \le N - 1)\)에 도구를 사용한다면 \(A_{1, i} + 1, A_{1, i + 1} + 1\)로 만들거나, \(A_{1,i}-1, A_{1, i+1} - 1\)로 만들거나, \(A_{1,i} + 1, A_{2, i} + 1\)로 만들거나, \(A_{1,i} - 1, A_{2, i} - 1\)로 만들 수 있는 도구이다. 이 도구는 얼마든지 사용할 수 있다.
• 일회용 도구: 행렬의 연속하는 \(j(2\le j \le N)\)개의 원소를 \(1\)만큼 증가시키거나 감소시키는 도구이다. 즉, \(A_{1,i}(1\le i \le N - 1)\)에 도구를 사용한다면, \(A_{1,i}+1, A_{1,i+1} + 1, \cdots , A_{1,i+j-1}+1\)로 만들거나 \(A_{1,i}-1, A_{1,i+1} - 1, \cdots , A_{1,i+j-1}-1\)로 만들거나, \(A_{1,i} + 1, A_{2, i} + 1\)로 만들거나, \(A_{1,i} - 1, A_{2, i} - 1\)로 만들 수 있는 도구이다. 이 도구는 한 번만 사용할 수 있다.

도구를 아무리 많이 사용하더라도 행렬 \(A\)를 행렬 \(B\)로 다듬을 수 없는 경우도 존재한다. 어떻게 다듬어야 하는지가 아니라 다듬는 것이 가능한지만 구해보자.

입력

첫째 줄에 정수 \(N(2 \le N \le 100\, 000)\)이 주어진다.

다음 두 줄에 걸쳐, 행렬 \(A\)의 각 원소가 주어진다. \((-1\,000 \le A_{r, c} \le 1\,000)\)

다음 두 줄에 걸쳐, 행렬 \(B\)의 각 원소가 주어진다. \((-1\,000 \le B_{r, c} \le 1\,000)\)

출력

행렬 \(A\)를 \(B\)로 다듬을 수 있다면 YES 를, 그렇지 않다면 NO를 출력한다. 모두 대문자로 출력해야하는 것에 유의한다.

예제 입력 1

4
1 2 3 4 
4 3 2 1
5 6 7 8
8 7 6 5

예제 출력 1

YES

예제 입력 2

5
1 -3 4 8 -3
4 2 -5 -7 6
2 12 -21 6 5
-2 3 8 7 -18

예제 출력 2

NO

예제 입력 3

4
8 -14 10 16
16 -5 -1 26
-15 -17 13 21
11 7 -22 10

예제 출력 3

YES